Решение простейших тригонометрических уравнений

1. cos x = a
Решение уравнения 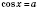будем искать, опираясь на рисунок 1 или рисунок 2.
Если 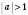, решений нет.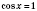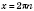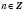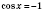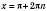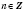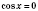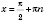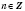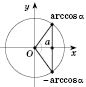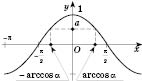
, , .
, , .
, , .


Рис. 2
Общий случай 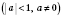: 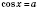, x = ±arccosa + 2πn,.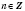
В случаях, когда 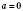, 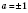, тоже можно пользоваться общей формулой, но это не так рационально.
Развязки, которые описываются общей формулой, можно разделить на две серии:
x1 = arccosa + 2πn, n Є Z;
x2 = -arccosa + 2πn, n Є Z.
2. sin x = a
Развязки будем искать, опираясь на рисунок 1 или рисунок 2.
Если 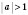, решений нет.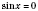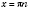
, , n Є Z.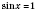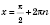
, , n Є Z.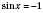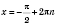
, , n Є Z.
Общий случай :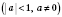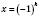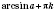
, k Є Z.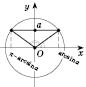

Рис. 1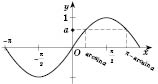

Рис. 2
Множество решений разбивается на две серии:
k = 2n, x1 = arcsina + 2πn, n Є Z;
k = 2n + 1, x2 = π - arcsina + 2πn, n Є Z.
3. tg x = a
Развязки запишем, опираясь на рисунок слева или на рисунок справа ниже.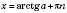
, n Є Z.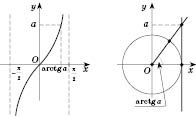

4. ctg x = a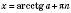
, n Є Z.
Если a = 0, 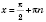, n Є Z.
Если 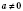, можно свести данное уравнение к уравнению .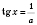
Примеры
1) ;
;
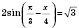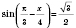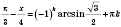, k Є Z;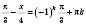
, k Є Z;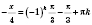
, k Є Z;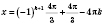
, k Є Z.
Множество решений можно разбить на две серии: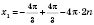
, n Є Z;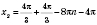
, n Є Z;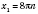
, n Є Z;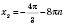
, n Є Z.
2) ;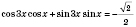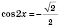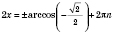
;
, n Є Z;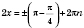
, n Є Z;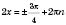
, n Є Z;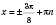
, n Є Z.